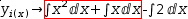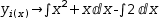4.2 Rearranging
Integrals and derivatives can be commuted, distributed and factored.
Left and right moves are used to rearrange operands within integrand and derivand as well as within integrator and derivator – when the latter are non trivial. This is the same as left and right moves in any other expression. However, interesting cases occur when the subject is at the extreme left or right of an integrand.
- When the subject of a move left (move right) is the leftmost
(rightmost) summand in an integrand or derivand, a move splits an
integral or derivative into the sum of two integrals or derivatives.
That is, applying ← to
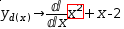
y_d(x)→ⅆ.{x^2}+x-2ⅆx yields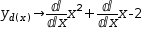
y_d(x)→ⅆx^2ⅆx+ⅆx-2ⅆx . - When the subject of a move left (move right) is the leftmost
(rightmost) multiplicand in an integrand or derivand, a constant can
be separated. That is, applying ← to
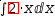
∫.{2}⋅x ⅆx yields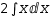
2⋅∫x ⅆx .
Distribute rearranges all the summands. Applied
to
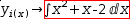
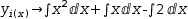

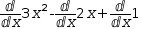
Factoring reverses these changes, providing a sort of inverse.
Applying Factor to